Intro

Paper infomation:

• Title: KAN: Kolmogorov–Arnold Networks
• Publication: Preprint on 2024.04.30 (Under Review)
• Authors: Ziming Liu*, el al.
• Affiliation: MIT, Caltech and NEU

Major contribution:

• generalizing(not invent! ) the K-A representation and revitalizing and contextualizing it in today’s deep learning word.
• using experiments to highlight its accuracy and interpretability.

Keywords

• K-A theorem based NN
  • KAT has been usded to construct NN since 1993 [10]
• Neural Scaling Laws [52, etc.]
• Mechanistic Interpretability(passive or active) [59, etc.]
• Learnable Activations [67, etc.]
• Symbolic Regression [73, etc.]
• AI for Mathematics [29, etc.]

K-A Representation Thm

Let be an arbitrary multivariate continuous function. Then it has the representation

where and are univariate functions. Note that:

• the inner functions are highly non-smooth.
• the outer functions depend on the specific function f and hence are not representable in a parameterized form.

but physicists don't care, just assume existence of smoothness

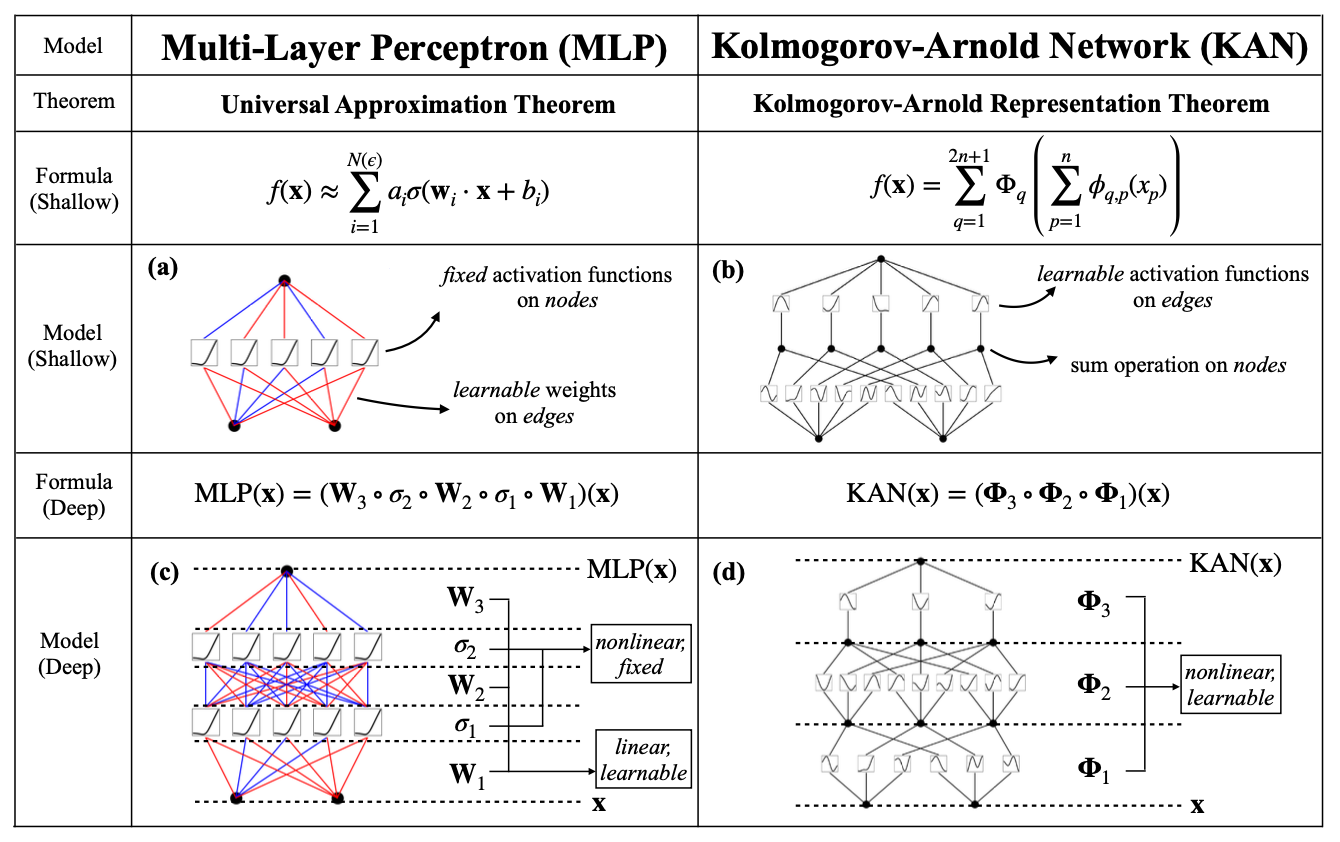
MLP v.s. KAN

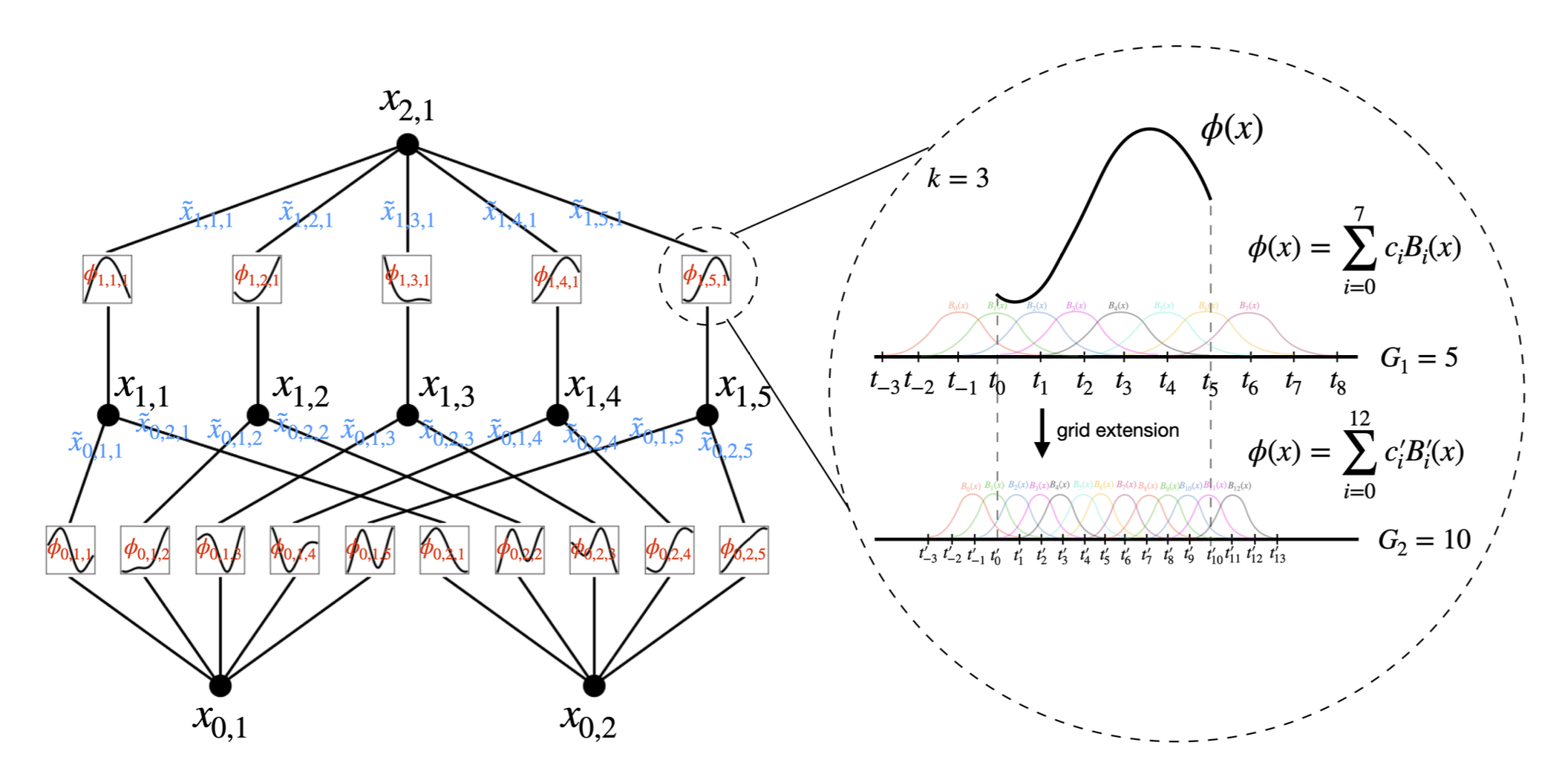
Recall B-spline

Spline function (of order k) :

• are knots on interval .
• is piecewise polynomial of degree on .
• at least.

B-spline of order k, which is basis function of splines of order k:

• add constraint
• can be constructed recursively:

KAN Implementation

• Model:
• approximation:
  • where is scale factor.
  • is Sigmoid Linear Unit function.
  • is linear combination of (cubic) B-splines, where are trainable weights.
• Initialization
  • .
  • with Xavier initialization.
• Update the spline grids on the fly, since activations vary.

Extension1

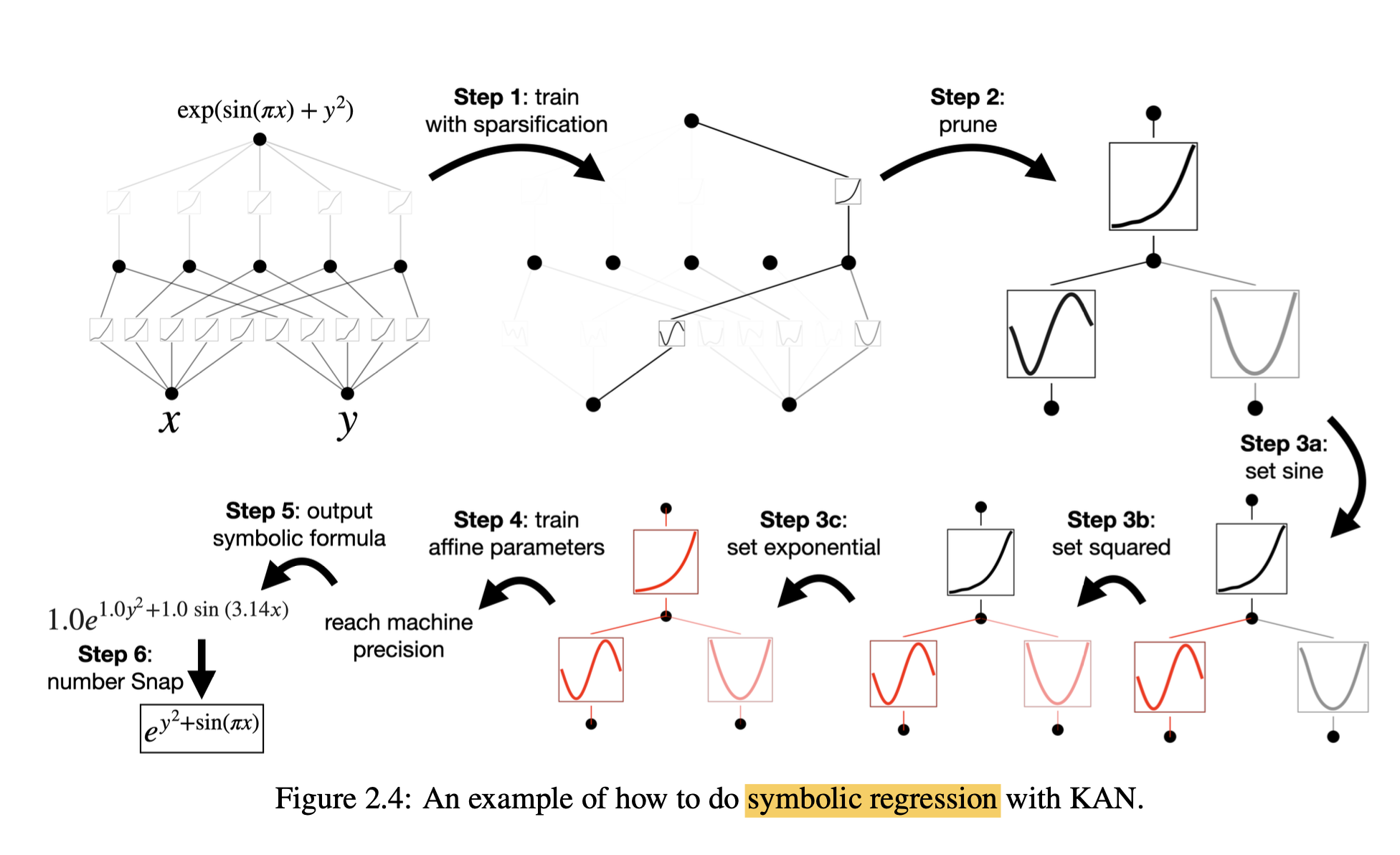
For Interpretability

• Sparsification loss( norm):

• Pruning by incoming and outgoing score threshold.

Extension1

Extension2

For Accuracy: finer grid

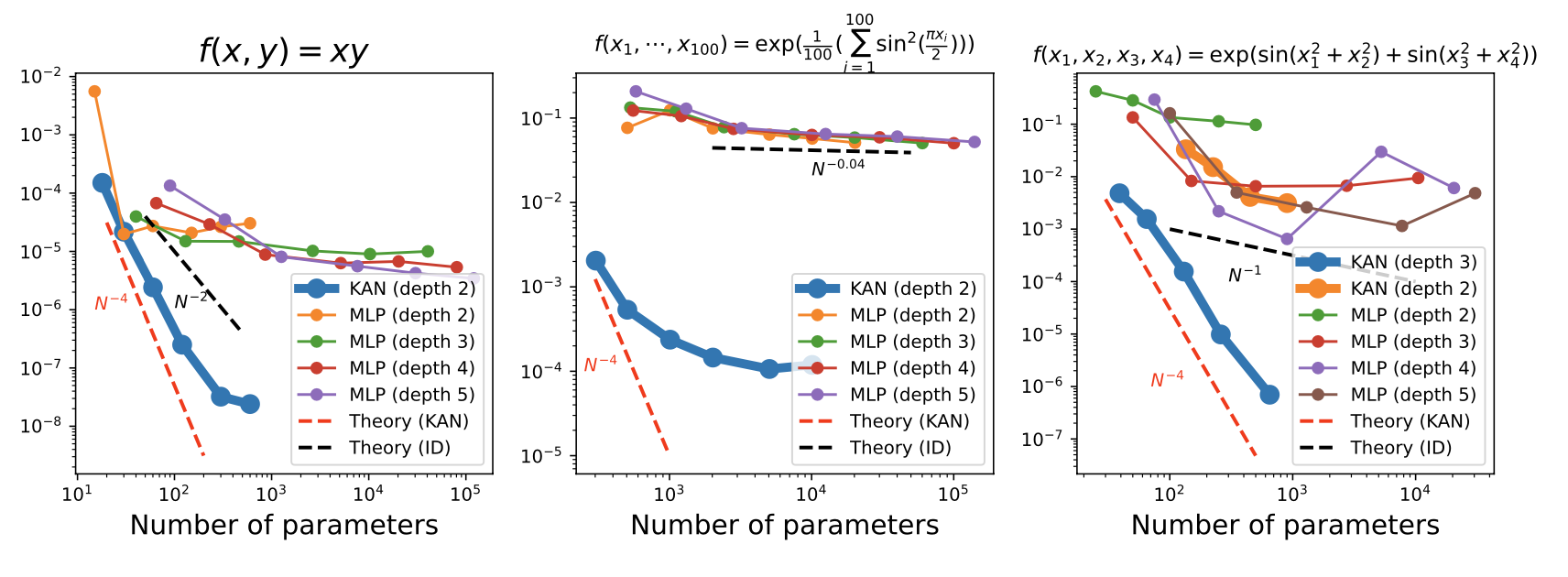
Neural Scaling Laws

Neural scaling laws are the phenomenon where test loss decreases with more model parameters:

where is RMSE, is num of parameters.

• KANs can empirically achieved bound .
• MLPs have problems even saturating slower bounds (e.g., ) and plateau quickly.

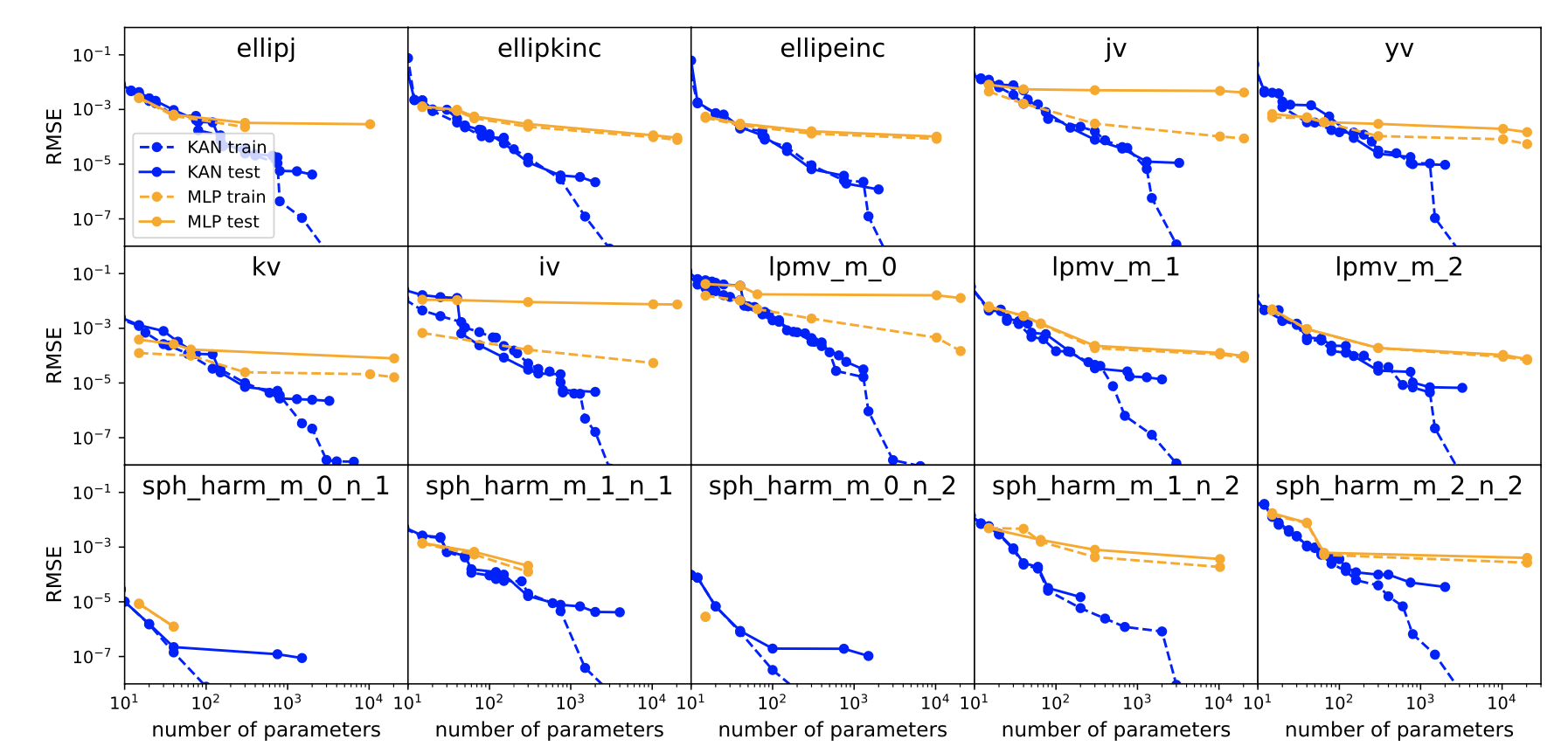
Experiment 1.1 simple functions

• have close form

Experiment 1.2 special functions

• no close form

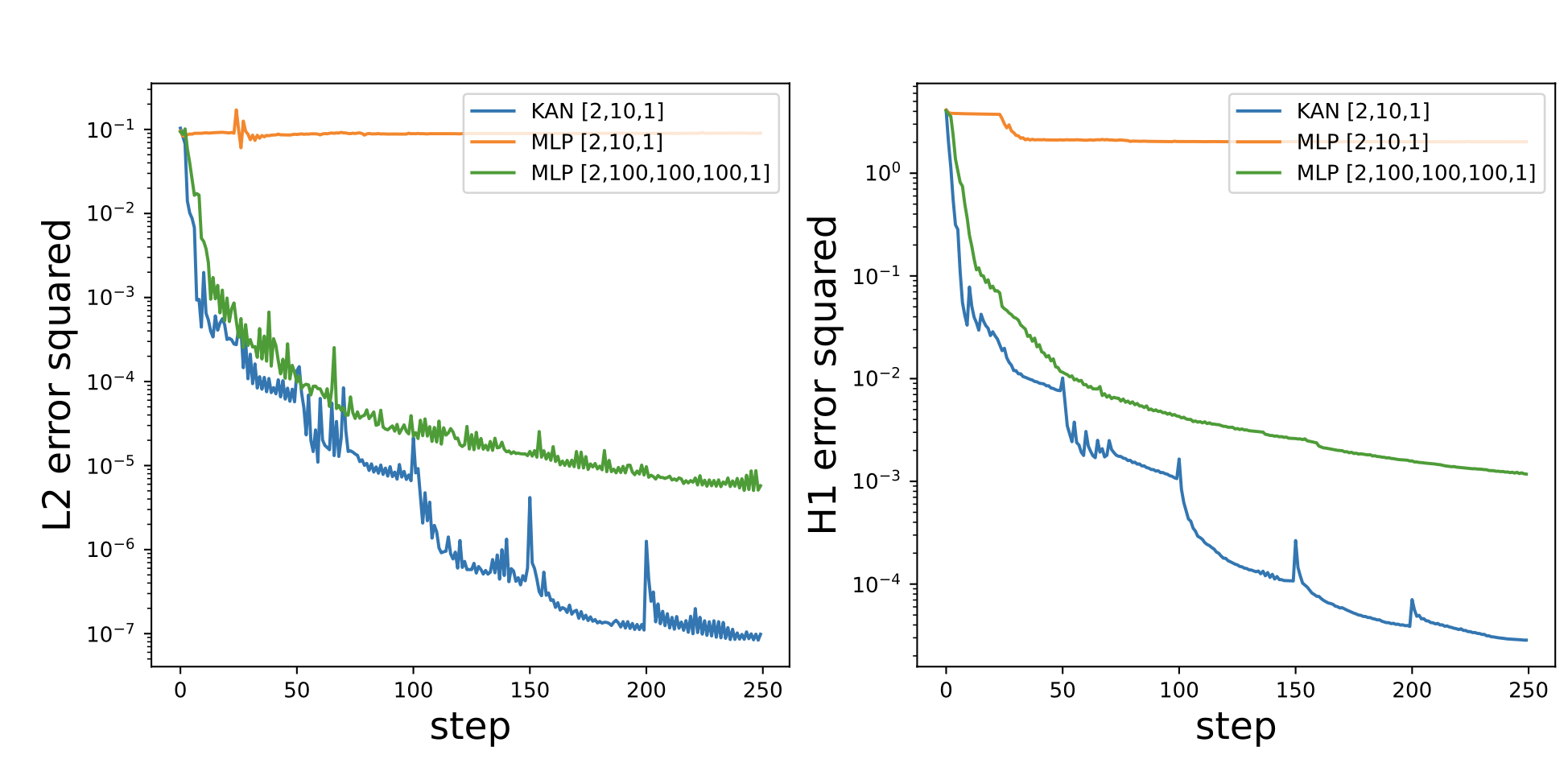
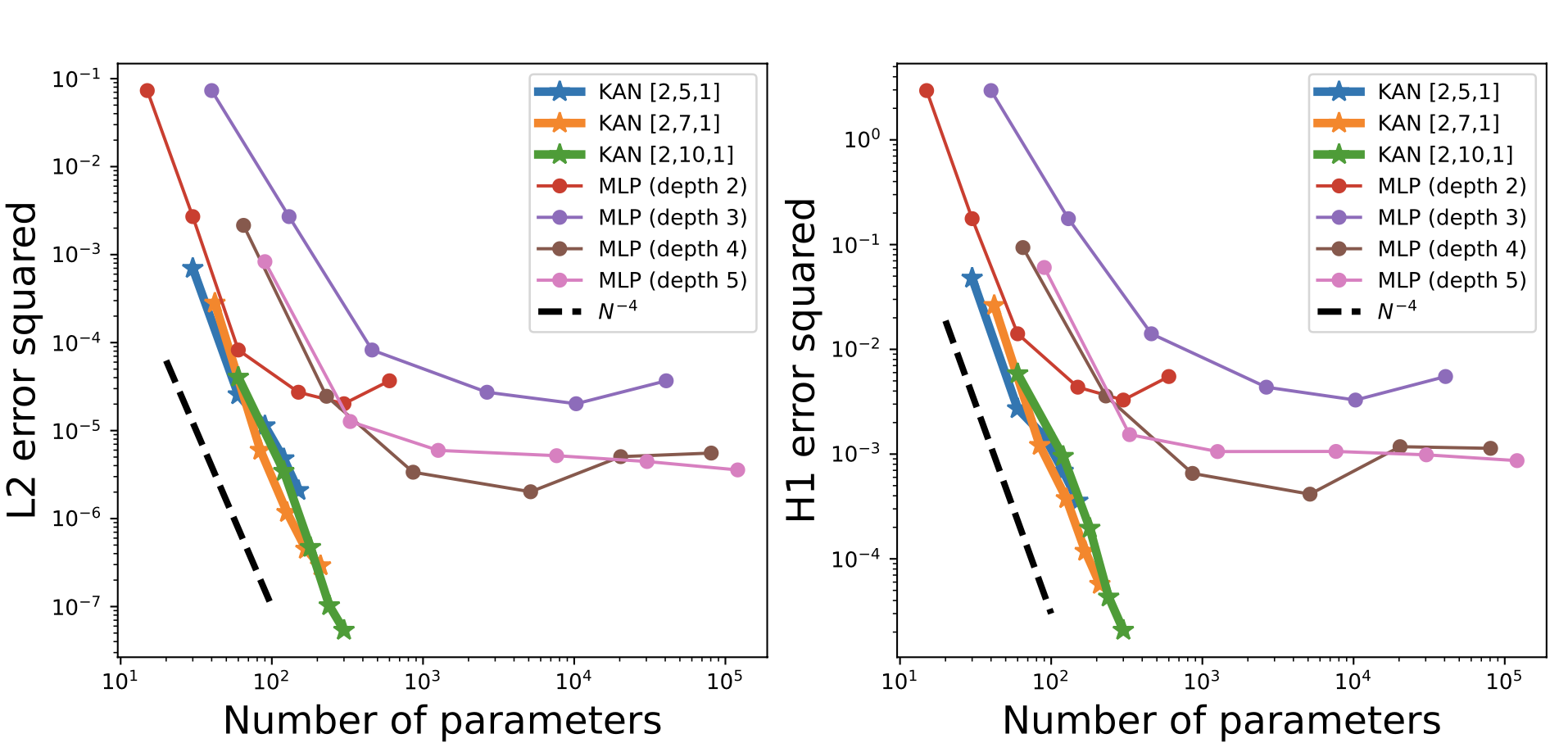
Experiment 2 Solving PDE

For

Consider data from

for which

is a true solution.

Consider training loss:

Experiment 2 Solving PDE

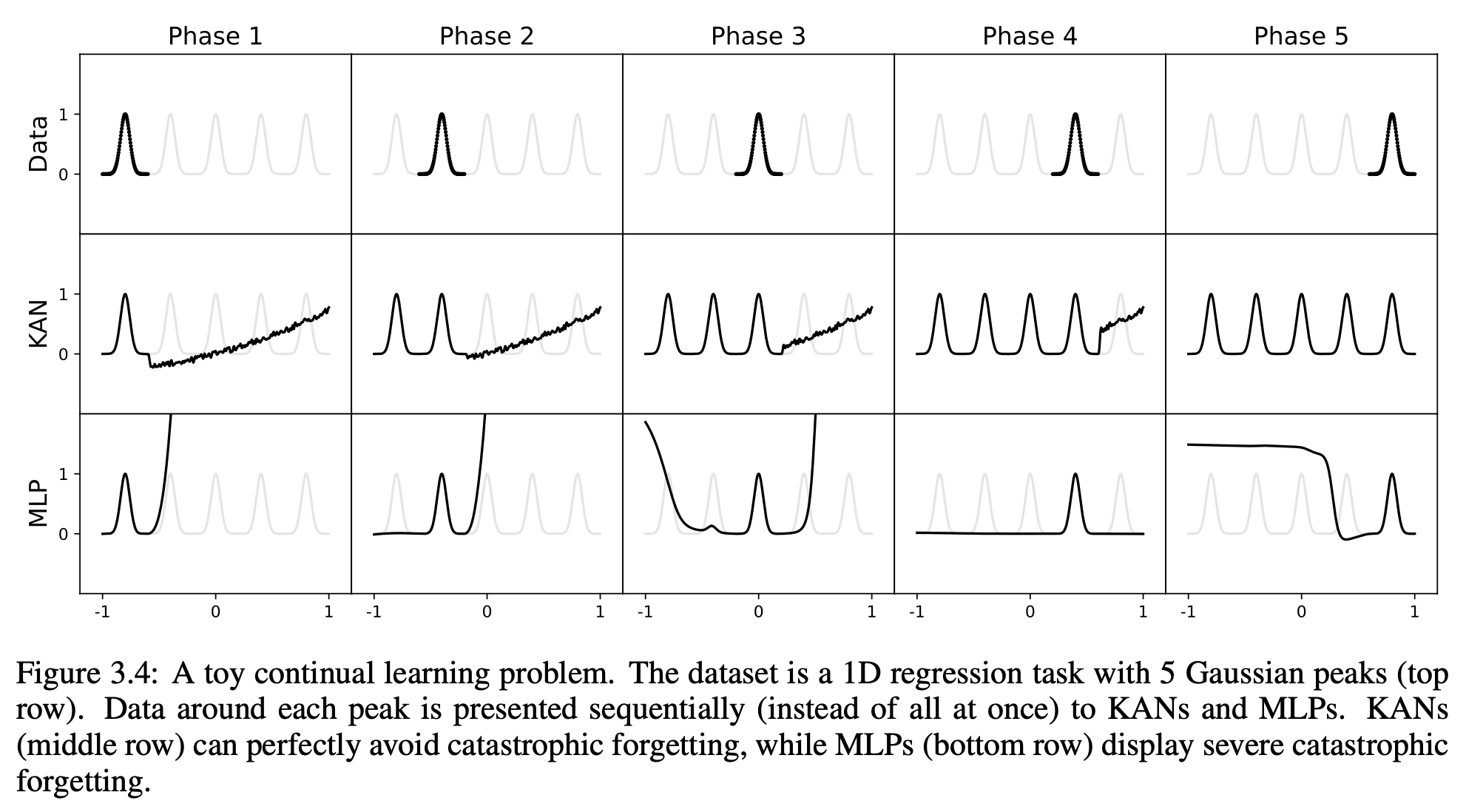
Experiment 3 Continual Learning?

Experiment 4 Supervised or not

• Supervised task: find s.t. (relationship between and )
• Unsupervised task: find s.t. (structural relationship between variables)
  • e.g. and are dependent, ind.

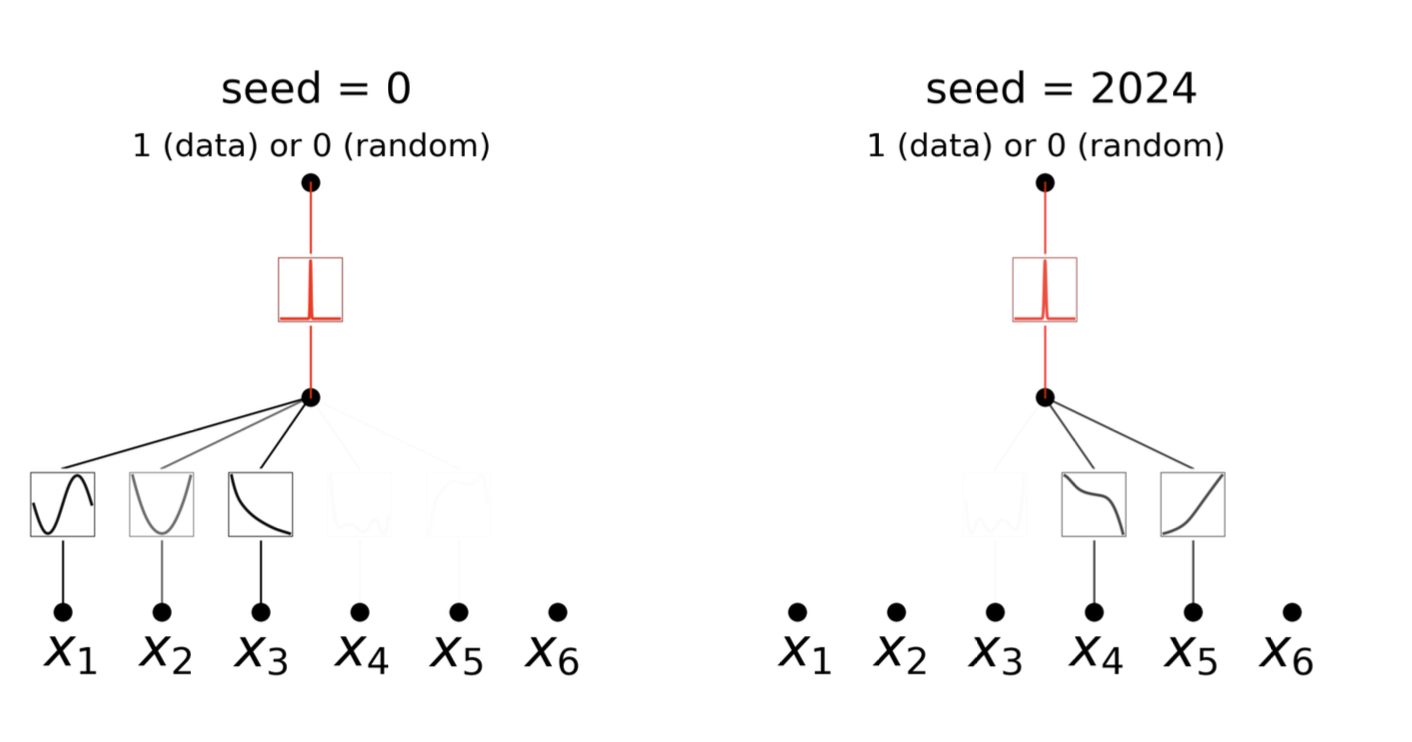
Application 1 Knot Theory (intro)

• How to do classfication?
  • by crossings: prime knots

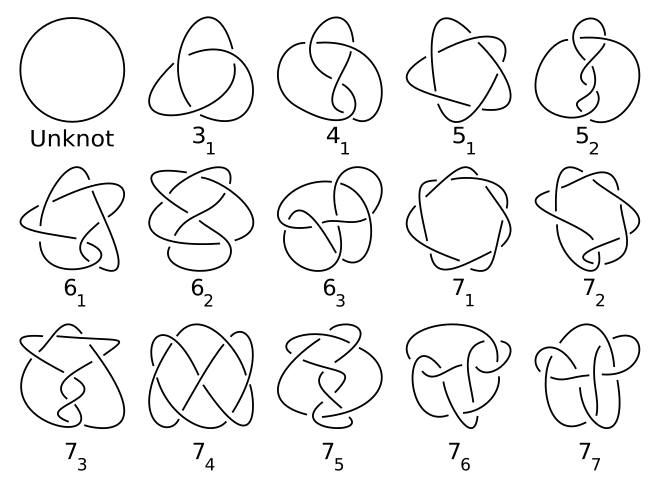
Application 1 Knot Theory (invariants)

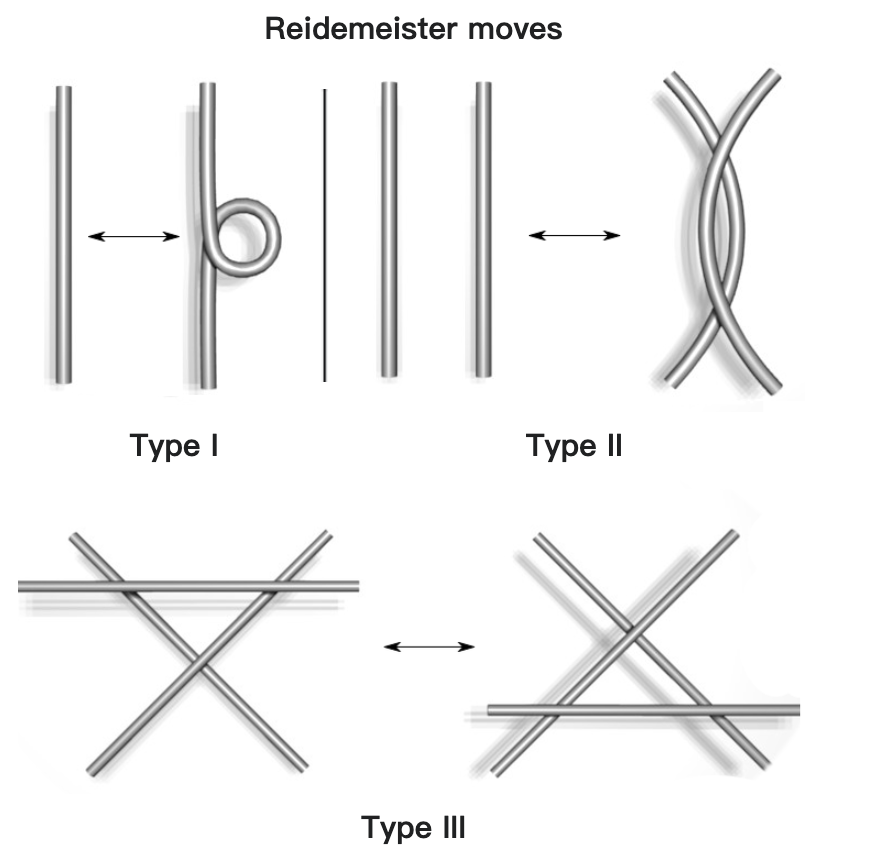
• Knots have a variety of deformation-invariant features f called topological invariants, e.g. Jones polynomial.
• basic deformation:

Application 1 Knot Theory(DeepMind)

• Davies, A., Veličković, P., Buesing, L. et al. Advancing mathematics by guiding human intuition with AI. Nature 600, 70–74 (2021). https://doi.org/10.1038/s41586-021-04086-x

Application 1 Knot Theory(results)

Two main results:

1. They use network attribution methods to find that the signature is mostly dependent on meridinal distance and longitudinal distance .

2. Human scientists later identified that has high correlation with the slope: and derived a bound for

KANs not only rediscover these results with much smaller networks and much more automation, but also present some interesting new results and insights.

Application 1 Knot Theory(KAN on 1.)

To investigate 1. , they treat 17 knot invariants as inputs and signature as outputs:

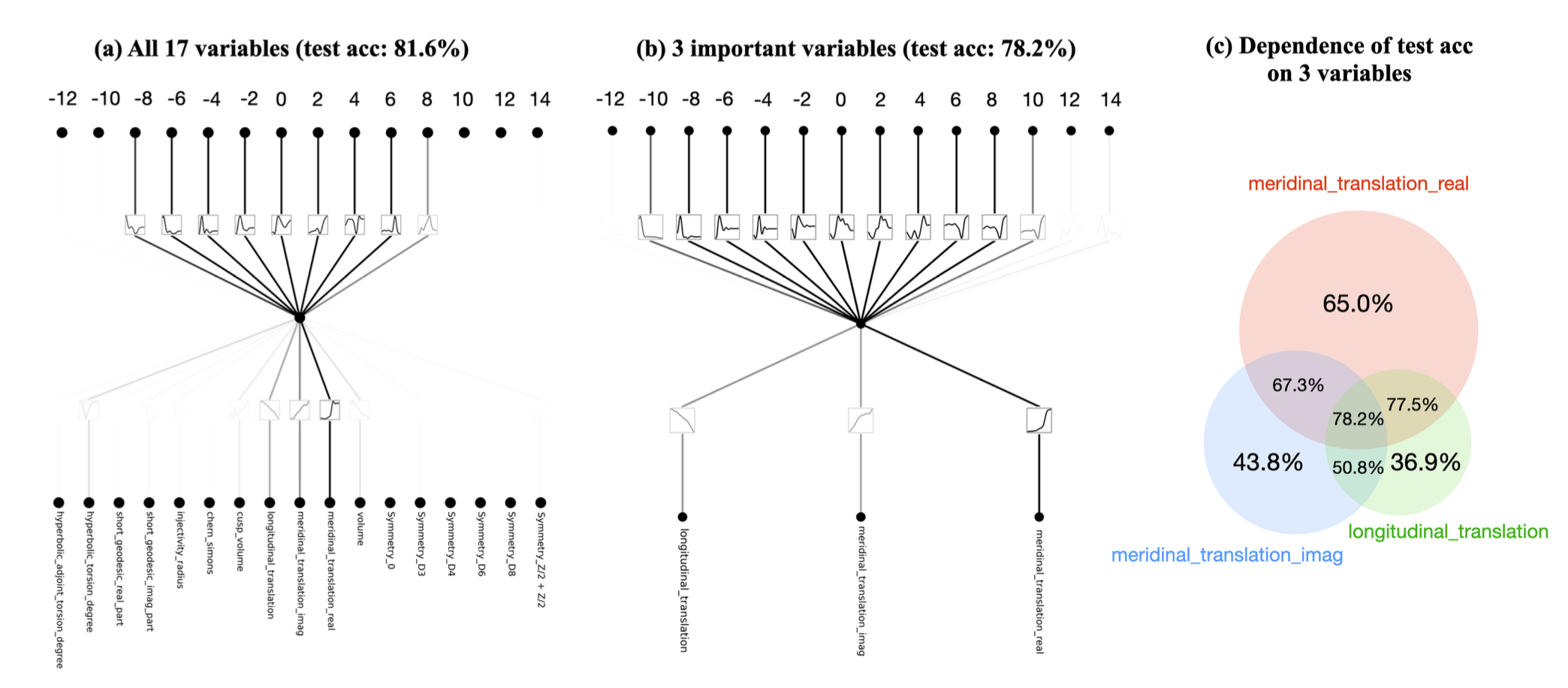
KANs have less parameters(2e2 v.s. 3e5), but behave better on accuracy(.816 v.s. .78).

Application 1 Knot Theory(KAN on 2.)

To investigate 2. ,they formulate the problem as a regression task.

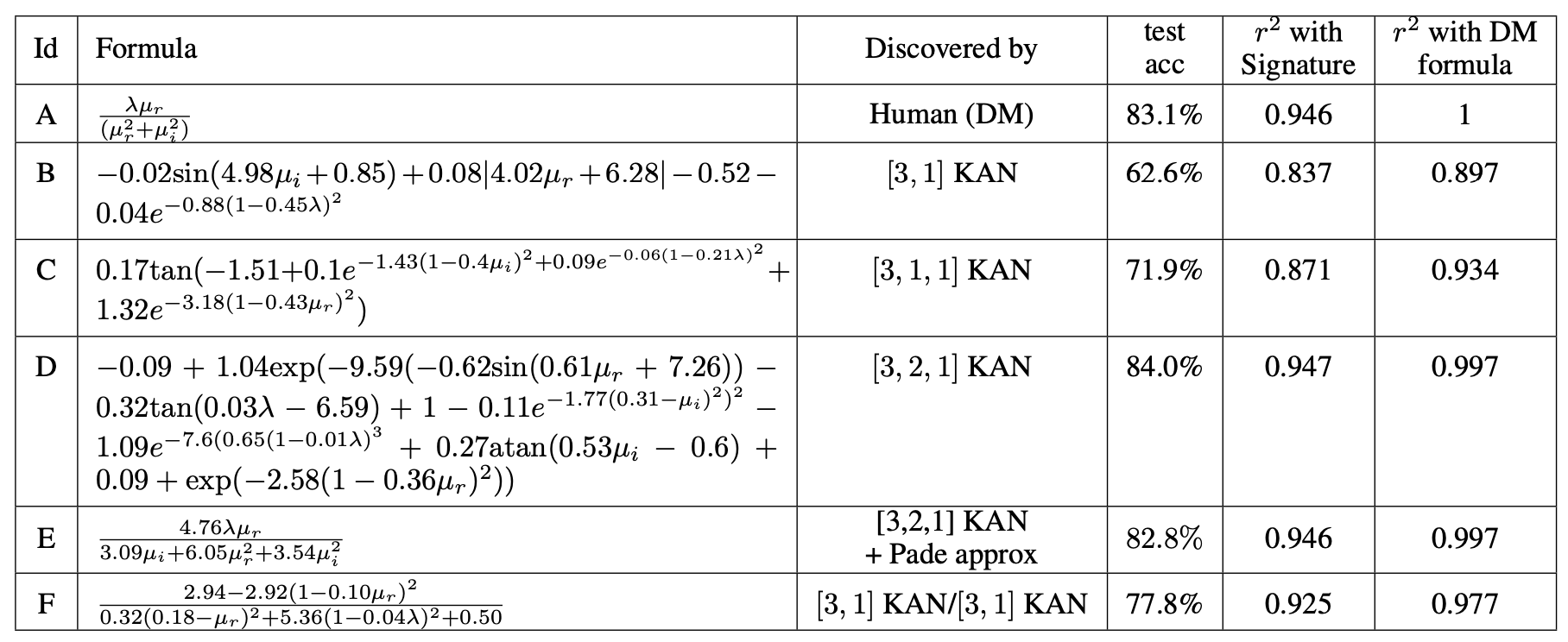
Application 1 Knot Theory(KAN new)

• KAN find some results:
  

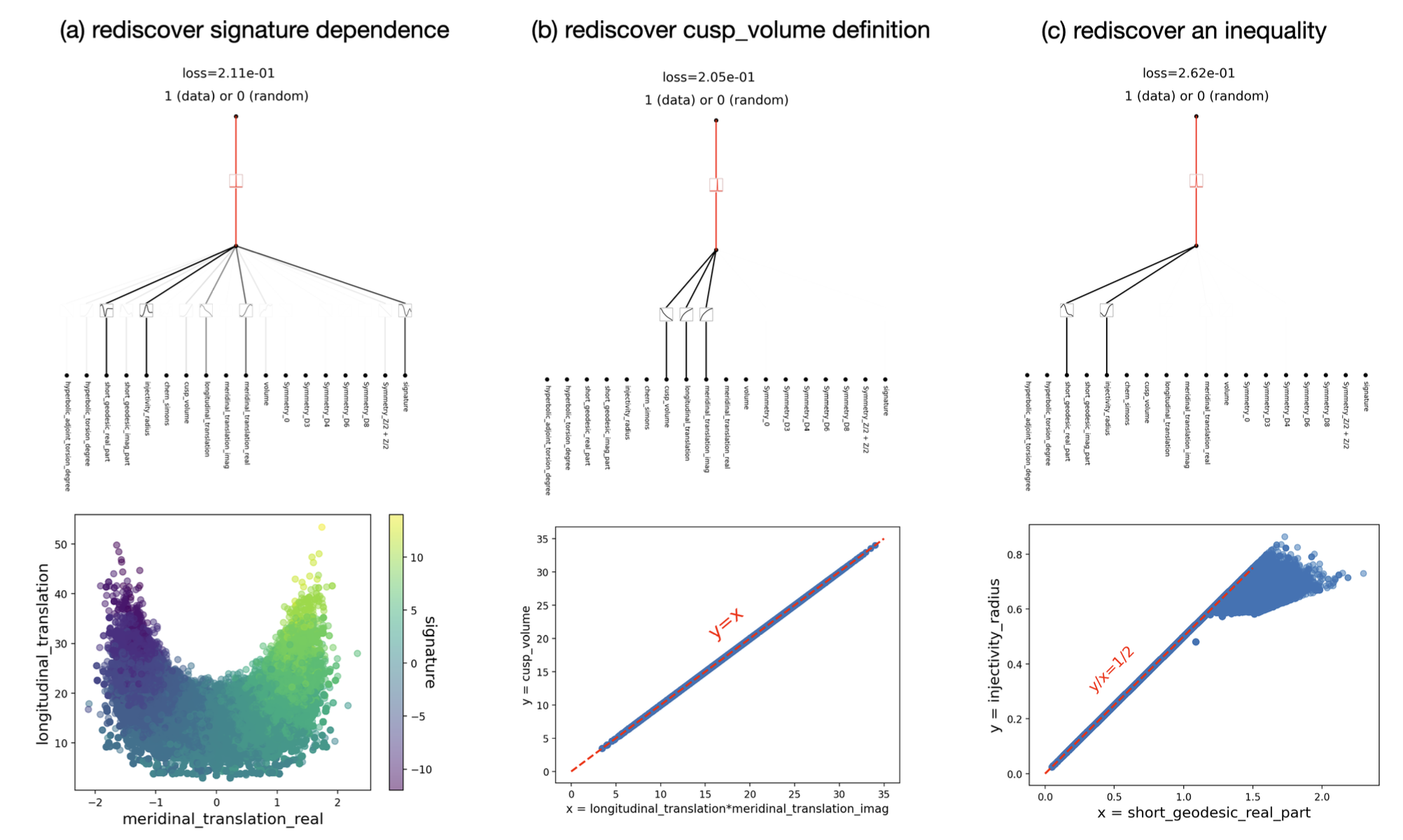
Application 2 Anderson Localization

Due to time constraints, we'll skip this part. TO MUCH PHYSICS!

so far so good, but ...

• KANs are usually 10x slower(in calculation) than MLPs given same num of parameters.

• Are KANs just RBF Networks? GitHub Issue#162

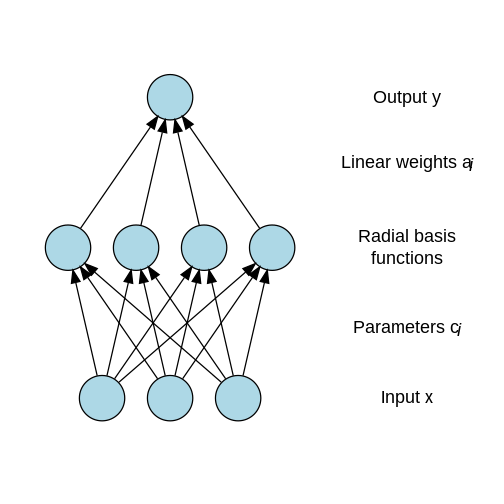
Discussion

• Since KANs work, maybe K-A theorem can be extended?
• Maybe we can use some other basis functions instead of B-splines, e.g. RBF, Fourier basis.
• Hybrid of KANs and MLPs, half fixed activation functions.
• KAN as a "language model" for AI + Science??

THANKS.