规矩数¶

今天我们来介绍一下规矩数。首先给出一个几何上的定义：

定义（规矩数，constructible number）：

如果一个数字$r$，它的绝对值$|r|$是在平面上可以用尺规作图作出的线段长度，那么$r$是规矩数。

什么是尺规作图¶

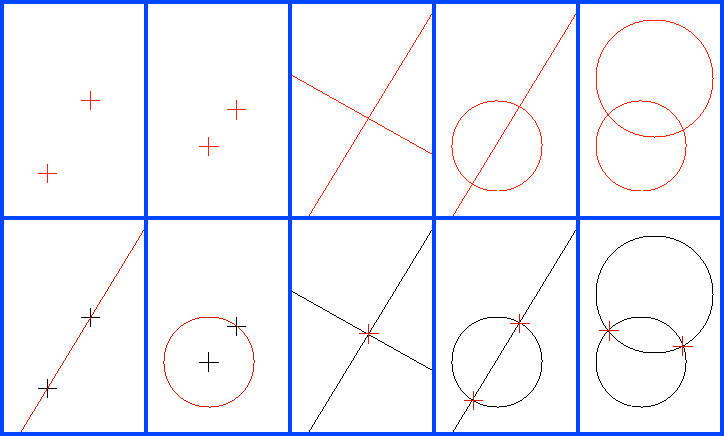
提到尺规作图大家应该是不陌生的，小学的时候大家都学过如何作角分线、垂直平分线等。一般而言尺规作图有五个作图公法（最基本的操作）：

1. 通过两个已知点可作一直线。
2. 已知圆心和半径可作一个圆。
3. 若两已知直线相交，可求其交点。
4. 若已知直线和一已知圆相交，可求其交点。
5. 若两已知圆相交，可求其交点。

在图上看来就是：

图源：https://www.geogebra.org/m/qb3jfzmy文中较为详细的介绍了各种尺规作图的方法，还有动画演示！下面平行线的作法也是这篇文章里截图的！

在此基础之上衍生出了一些其他的作图方法。

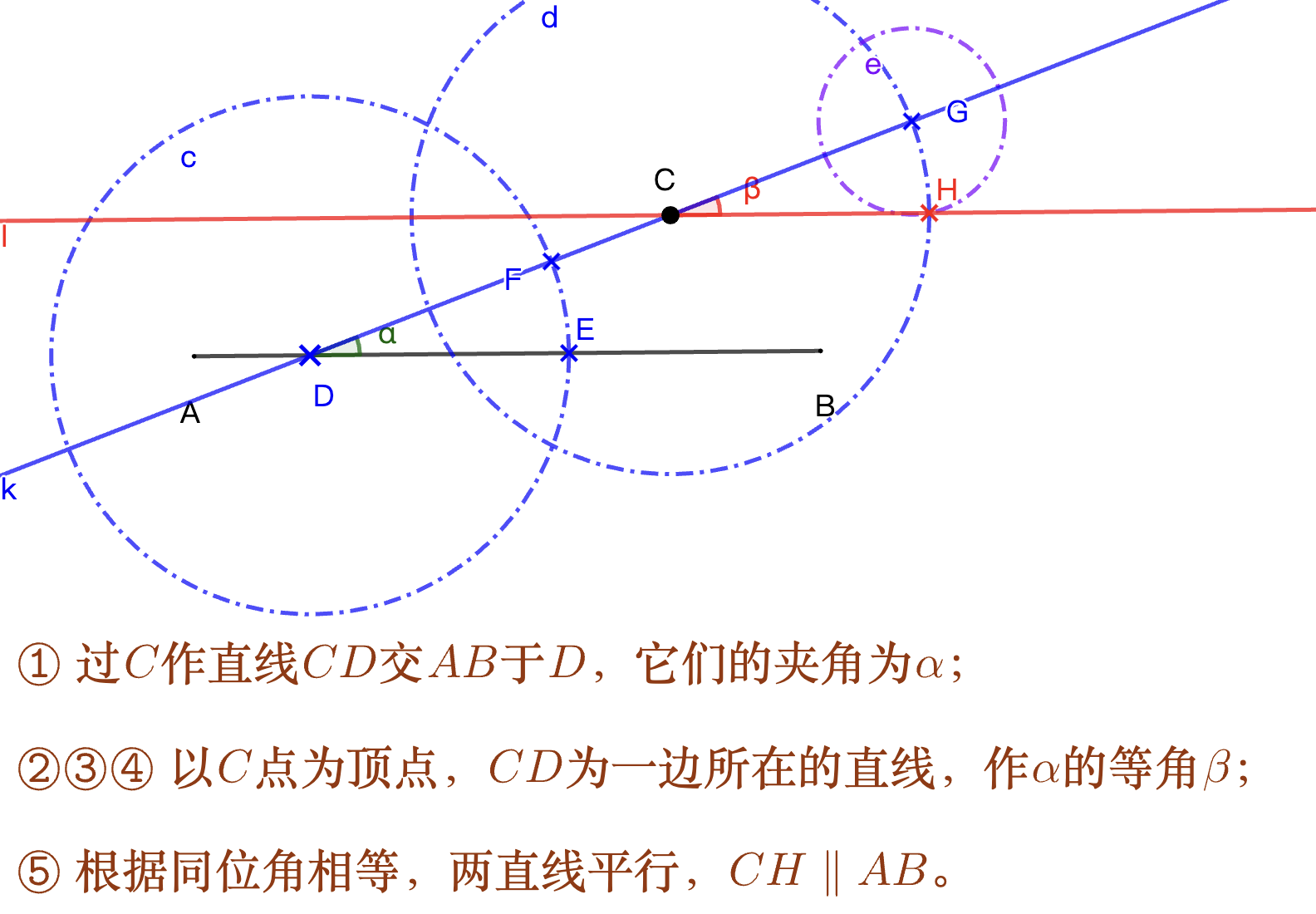
尺规作平行线¶

平行线的作法比较重要，我们放张图在这里，大家可以比划比划：

其他的操作：作角分线，作垂直平分线等这里就不再赘述。

有理数都是规矩数¶

不难证明，所有的整数都是规矩数，我们很容易从单位长度1的线段（通过延长线段）得到长度为任意整数的线段。

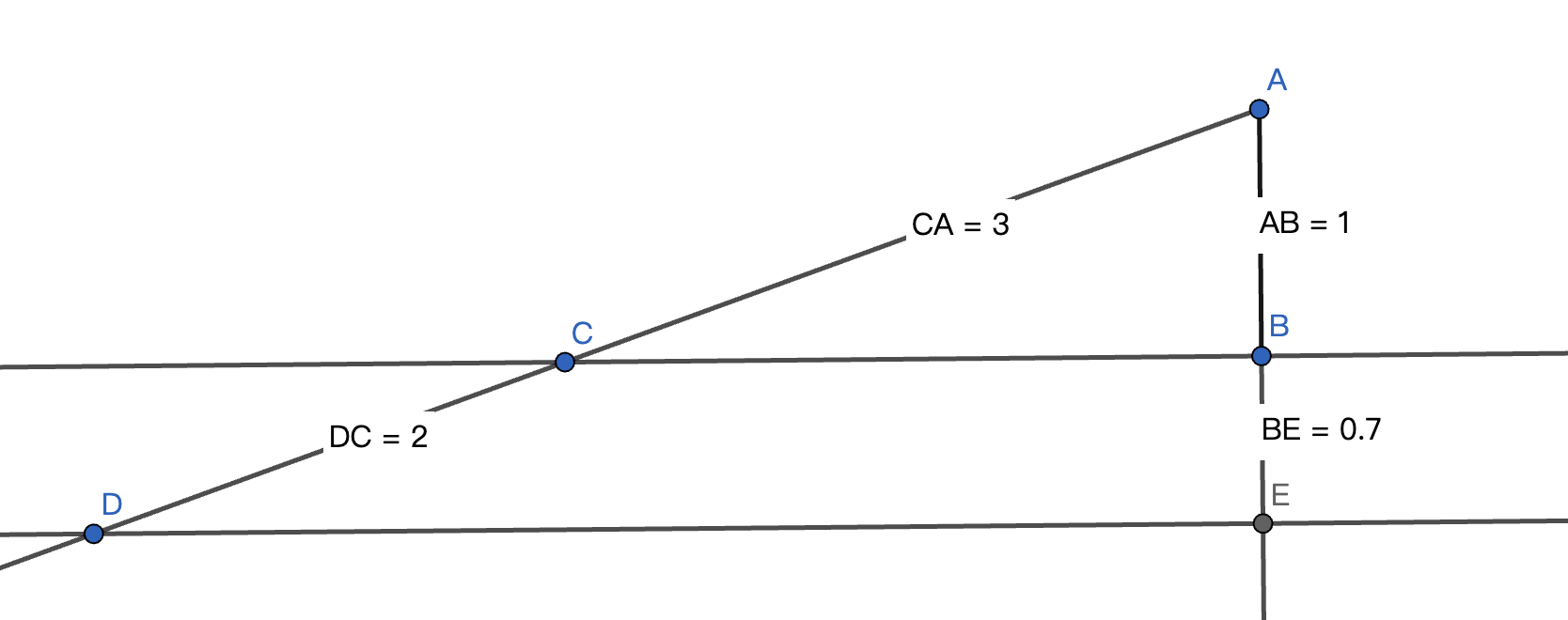
然后利用平行线的作法，我们就可以从$m,n$得到$n/m$，具体如下图（或许叫平行线分线段成比例定理）：

图中$AC=3$，$CD=2$，如果$AB=1$那么就得到$BE=2/3$

作图的顺序是：

1. 先作线段$AB$，长度作为1
2. 作过$B$和$AB$垂直的直线$l$
3. 用圆规在直线$l$上找一点$C$使得$AC=3$
4. 延长$AC$到$D$使得$CD=2$
5. 过$D$作$CB$的平行线$k$
6. 延长$AB$交直线$k$于$E$点

规矩数域¶

尺规开二次方¶

上一节我们说明了所有的有理数都是规矩数，但规矩数远不止于此。例如$\sqrt{2}$就是一个典型的无理数，但它是一个规矩数：我们很容易作出一个直角边为$1$的等腰直角三角形，那么它的斜边长度就是$\sqrt{2}$。

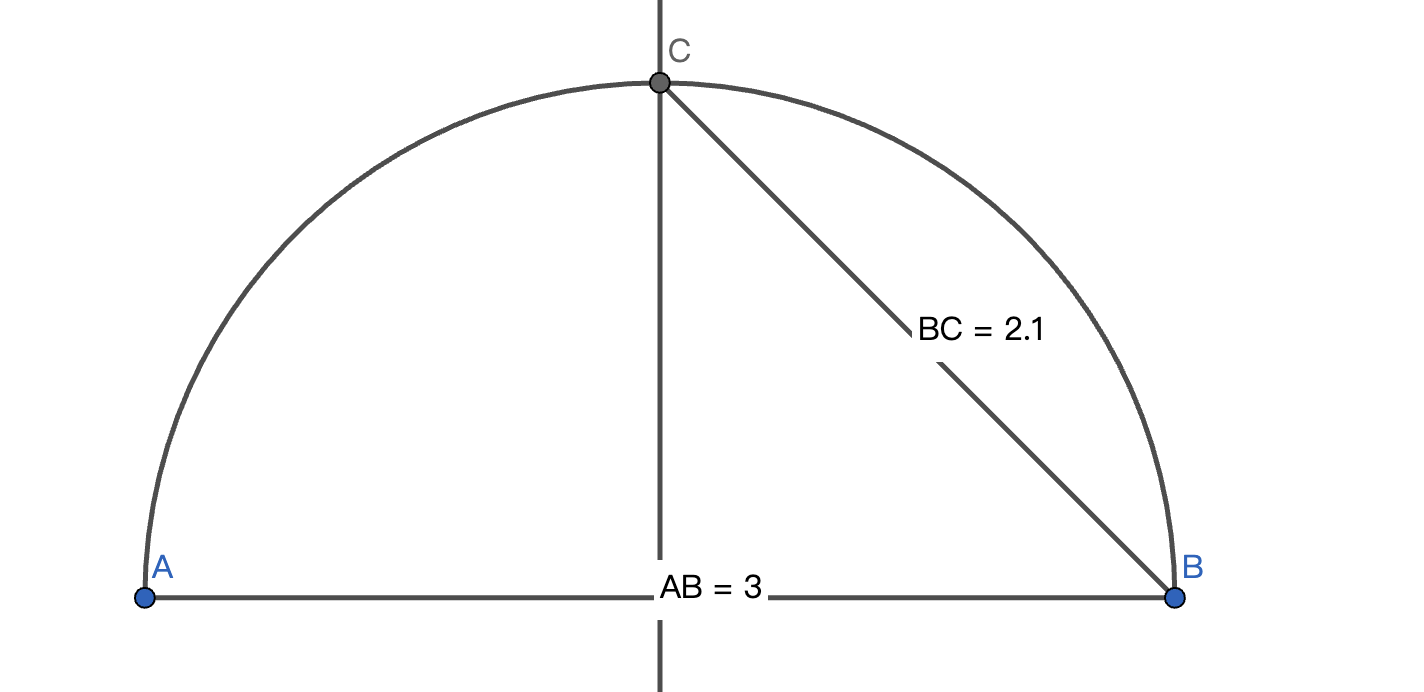
更进一步的，我们还可以在尺规作图中实现开二次方的运算：

作图的顺序是：

1. 作定长线段$AB=3$
2. 作$AB$的垂直平分线，和以$AB$为直径的圆相交于点$C$
3. 得到$BC=\sqrt{3}$

那么，所有的规矩数构成的集合有什么特点呢？？在代数学中我们有一个结构刚好可以描述它，那就是域。

域是在集合上定义了加法和乘法两个二元运算的代数结构：$(\mathbb{F},+,\times)$，满足：

• 它在加法下是交换群
• 它在乘法下除了零元外构成交换群（也即是非零元都可逆）
• 乘法和加法相容（有乘法分配律）：$a\times(b+c)=a\times b+a\times c$

那么你可能又要问，什么是交换群？

交换群是特殊的群，如果在一个集合$\mathbb{G}$上定义了二元运算（例如加法），满足： - 结合律：$(a+b)+c = a+(b+c)$

• 有单位元：$\exists 0 \in G$，使得$\forall a\in G$都有$a+0=a$

• 有逆元：$\forall a\in G, \exists -a\in G \quad a+(-a)=0$

• 交换律：$a+b=b+a$

那么$\mathbb{G}$是一个交换群。

大家可以自行验证上面的各条性质。我这里验证比较重要的一条：

规矩数域的封闭性¶

• 对加减乘除封闭是交换群的要求，显然如果$a,b$都是规矩数，那么$a\pm b$、$a*b$和$a/b$都是规矩数。

  • 加减法自然不必说，尺规作图中只要延长或者截断即可。除法我们之前用平行线实现了，乘法类似：$a*b$相当于$a*(1/b)$，那么我们只需要先作出$1/b$，然后再和$a$做一次除法即可。

• （非负元）对开二次方封闭是规矩数域特有的一个性质，如果$a$是（非负的）规矩数，那么$\sqrt{a}$也是规矩数。

  • 前面我们展示了尺规作图如何对任何的长度开二次方

规矩数的一个子域¶

$$ \mathbb{Q}(\sqrt{2})=\left\{x\mid x=a+b\sqrt{2}\quad a,b\in\mathbb{Q}\right\} $$ 这是常见的一个域的例子，大家可以比划比划，验证上面提到的域的各个条件。

域的扩张¶

不难发现，$\mathbb{Q}(\sqrt{2})$其实就是在有理数域中添加了一个元素$\sqrt{2}$得到的域，我们把这种操作叫做域的扩张。

在尺规作图中，我们一旦作出了一个长度，就可以在以后的作图中继续使用这个长度。

例如，我们作出了$\sqrt{2}$的长度，那么后续可以作$1+3\sqrt{2}$等，“我们能作出的长度”一下子增加了很多。

我们就说：作$\sqrt{2}$引起了域的扩张。

根据线性代数的知识，可以验证$\mathbb{Q}(\sqrt{2})$是$\mathbb{Q}$上的一个线性空间，并且$\{1,\sqrt{2}\}$恰可以成为这个域上的一个基（也就是说该域中的所有元素都可以表示为它们的线性组合$a*1+b*\sqrt{2}$），所以它的维度 $$ \dim \mathbb{Q}(\sqrt{2})=2 $$

故称它是有理数域的二次扩张，记作$\mathbb{Q}(\sqrt{2})/\mathbb{Q}$，扩张次数记作$[\mathbb{Q}(\sqrt{2}):\mathbb{Q}]=2$。值得一提的事，有理数域是“最小的”数域，它是任何其他数域的子集。或者说任何其他数域都是它的扩张。

在尺规作图中，如果你作出了$\sqrt{2}$这个长度，就会引起域的二次扩张。

到坐标系中¶

下面我们建立平面直角坐标系，用解析几何来回答：哪些数是规矩数，规矩数有什么特点？

不难证明：坐标系中一个点$(a,b)$是规矩的（可以尺规作图），当且仅当他的每个坐标都是规矩数。

如果$a,b$是规矩数，那么这个点可以通过$y$轴平行线$x=a$和$x$轴平行线$y=b$的交点来确定的。

反之如果已知这个点的位置，也可以作垂线来确定$a,b$在坐标轴上的位置，那么$a,b$是规矩数。

而根据我们前面所说的五条作图公法，尺规作图中产生点有以下几个方法：

• 在直角坐标系中直接点出来（需要坐标都是规矩数）
• 直线和直线的交点
• 直线和圆的交点
• 圆和圆的交点

下面我们来研究这几个操作的后果。

尺规作图画出的直线和圆¶

尺规作图用两点确定一个直线，设$l$过两点$(x_1,y_1)$和$(x_2,y_2)$，那么它的方程为 $$ (y-y_1)(x_2-x_1)-(x-x_1)(y_2-y_1)=0 $$ 其中$x_{1,2}$和$y_{1,2}$都是规矩数。稍作整理： $$ (y_1-y_2)x+(x_2-x_1)y+y_1(x_1-x_2)+x_1(y_2-y_1)=0 $$ 根据前面所说，规矩数对加减乘除都是封闭的，那么上式也就可以表示成： $$ ax+by+c=0 $$ 其中$a,b,c$是规矩数。

类似的，圆的方程： $$ (x-x_0)^2+(y-y_0)^2=d^2 $$ 可以表示成： $$ x^2+y^2+ax+by+c=0 $$ 其中$a,b,c$是规矩数。

直线和直线的交点¶

两条直线联立，得到一个一次方程，它的根必然是由系数的加减乘除构成的，而规矩数域是对加减乘除封闭的，所以域没有发生变化。

圆和圆的交点¶

方程： $$ \left\{ \begin{aligned} &a_1x+b_1y+c_1+x^2+y^2=0\\ &a_2x+b_2y+c_2+x^2+y^2=0 \end{aligned}\right. $$ 相当于直线和圆的交点： $$ \left\{ \begin{aligned} &(a_1-a_2)x+(b_1-b_2)y+c_1-c_2=0\\ &a_2x+b_2y+c_2+x^2+y^2=0 \end{aligned}\right. $$

直线和圆的交点¶

方程： $$ \left\{ \begin{aligned} &a_1x+b_1y+c_1=0\\ &a_2x+b_2y+c_2+x^2+y^2=0 \end{aligned}\right. $$ 是一个二次方程，所得的（实数）根都是： $$ a\pm b\sqrt{c} $$ 的形式，其中$a,b,c$都是规矩数。

也就是说，直线和圆的交点最多会产生一个新的二次根号元素：$\sqrt{c}$，换言之这个操作引起的域扩张是这样的： $$ \mathbb{Q} $$ $$ F_1=\mathbb{Q}(\sqrt{a})\quad a>0,a\in\mathbb{Q},\sqrt{a}\notin \mathbb{Q} $$ $$ F_2=F_1(\sqrt{b})\quad b>0,b\in F_1,\sqrt{b}\notin F_1 $$ 依此类推。当然，也有可能解出来的根恰好可以开方，域不会扩张。

不难证明，每次域扩张的次数都是$2$，累计起来，相对于$\mathbb{Q}$的扩张次数为$2^n$

举例来说，域$\mathbb{Q}(\sqrt{2})$，添加一个元素$\sqrt{3}$得到$\mathbb{Q}(\sqrt{2},\sqrt{3})$

那么 $$ \mathbb{Q}(\sqrt{2},\sqrt{3})=\{x|x=a+b\sqrt{3}\quad a,b\in\mathbb{Q}(\sqrt{2})\} $$ 显然$\{1,\sqrt{3}\}$是$\mathbb{Q}(\sqrt{2},\sqrt{3})$在$\mathbb{Q}(\sqrt{2})$上作为线性空间的一组基底，所以扩张次数是： $$ [\mathbb{Q}(\sqrt{2},\sqrt{3}):\mathbb{Q}(\sqrt{2})]=2 $$

此外不难验证，$\mathbb{Q}(\sqrt{2},\sqrt{3})$中所有的元素都可以写成： $$ a+b\sqrt{2}+c\sqrt{3}+d\sqrt{6}\quad a,b,c,d\in \mathbb{Q} $$ 所以$\{1,\sqrt{2},\sqrt{3},\sqrt{6}\}$是$\mathbb{Q}(\sqrt{2},\sqrt{3})$在$\mathbb{Q}$上作为线性空间的一组基底，所以扩张次数是： $$ [\mathbb{Q}(\sqrt{2},\sqrt{3}):\mathbb{Q}] = 4 $$ 实际上可以证明域的扩张次数满足公式： $$ [F_1:F_3] = [F_1:F_2]*[F_2:F_3] $$

尺规作图的效果¶

综上所述，尺规作图就是从有理数域开始做一系列域扩张，每次扩张的次数都是$2$： $$ \mathbb{Q}\subset F_1\subset F_2\subset \cdots $$ 所以有 $$ [F_n:\mathbb{Q}]=2^n $$

上回说到¶

我们在介绍复数的来历时提到了规矩数。并且我们说$\cos(\pi/9)$不是一个规矩数，所以它必须用复数才能表示。

很抱歉这个说法是错误的。

$\cos(\pi/9)$确实不是规矩数，但这只是表明它是无法用有理数的有限次的加减乘除和开二次方运算来表示。如果想要证明它不能用实数的加减乘除乘方运算表示（从而引出复数的必要性），还需要进一步的证明（这要困难得多）。

举例来说，$\sqrt[3]{2}$不是规矩数，但是它显然可以用实数（的加、减、乘、除、乘方）来表示。

但我们还是来证明一下$\cos(\pi/9)$不是一个规矩数

域扩张的视角¶

设$a=\cos(\pi/9)$，那么 $$ \mathbb{Q}(a)=\{z:z=x+\sum_i y_ia^{k_i}\quad x,y_i\in \mathbb{Q}\quad k\in \mathbb{N}\} $$

请注意这里集合的写法，之前我们写的扩张域都是写成： $$ \mathbb{Q}(\sqrt{2})=\{x|x=a+b\sqrt{2}\quad a,b\in \mathbb{Q}\} $$ 这一点其实没有那么直接，因为所谓的扩张域是“把一个元素加入之后，对加减乘除法构成封闭的集合”，只不过很容易验证，它可以写成上面的集合。但是$\cos(\pi/9)$要特殊的多，我们需要写出上述较为一般的形式。

根据三倍角公式，$a$是下述方程的一个根： $$ 8a^3-6a=1 $$ 可以证明： $$ \{1,a,a^2\} $$ 是$\mathbb{Q}(\cos(\pi/9))$的一组基底。所以这个域的扩张次数$[\mathbb{Q}(\cos(\pi/9)):\mathbb{Q}]=3$

证明基底需要一些线性代数的知识，我们先使用反证法来说明它们线性无关：

假设$\{1,a,a^2\}$是线性相关的，那么在数域$\mathbb{Q}$上存在不全为0的$k_{1,2,3}$使得： $$ k_1+k_2a+k_3a^2=0 $$ 如果$k_3=0$，那么 $$ a=-\frac{k_1}{k_2} $$ 是有理数。

如果$k_3\ne0$，那么可以同除$k_3$： $$ a^2+k_2a/k_3+k_1/k_3=0 $$ 两边同乘$a$： $$ 8a^3+8k_2a^2/k_3+8k_1a/k_3=0 $$ 代入$8a^3-6a=1$得到： $$ \frac{8k_2}{k_3}a^2+(\frac{8k_1}{k_3}+6)a+1=0 $$ 再把$a^2+k_2a/k_3+k_1/k_3=0$代入得到： $$ -\frac{8k_2}{k_3}(\frac{k_2}{k_3}a+\frac{k_1}{k_3})+(\frac{8k_1}{k_3}+6)a+1=0 $$ 显然这是一个系数都是有理数的一次方程，也可以得到$a$是一个有理数。

但是方程： $$ 8a^3-6a=1 $$ 是不存在有理数根的。这一点同样可以用反证法来说明：

假设$a$是一个有理数，他可以表示成既约分数： $$ a=\frac{p}{q} $$ 其中是互质的整数，$(p,q)=1$，回代到方程中得到： $$ \frac{8p^3}{q^3}-\frac{6p}{q}=1 $$ 整理成： $$ 8p^2-6q^2=\frac{q^3}{p} $$ 等式左侧是一个整数，然而等式右侧一定不是整数，因为$(p,q)=1$，它们没有公因子。

故而矛盾产生，假设不成立，$a$不是有理数。

所以我们最初的假设也不成立，$\{1,a,a^2\}$应该是线性无关的。

并且 $$ a^3=\frac{1}{8}+\frac{3}{4}a $$ 是可以被线性表出的。

以此类推，更高的次幂可以不断降幂，从而： $$ \forall z\in\mathbb{Q}(a)=\{z:z=x+\sum_i y_ia^{k_i}\quad x,y_i\in \mathbb{Q}\quad k\in \mathbb{N}\} $$ 都可以被$\{1,a,a^2\}$线性表出。

所以$\{1,a,a^2\}$是一组基底，空间的维度为： $$ \dim \mathbb{Q}(\cos(\pi/9)) =3 $$

最终答案¶

至此，我们大概就能说明$\cos(\pi/9)$不是规矩数了，域$\mathbb{Q}(\cos(\pi/9))$的扩张次数为： $$ [\mathbb{Q}(\cos(\pi/9)):\mathbb{Q}]=3 $$ 然而尺规作图生成的域$F_n$的扩张次数为： $$ [F_n,\mathbb{Q}]=2^n $$ 所以$\cos(\pi/9)$的长度不可能通过尺规作图得到，所以它不是规矩数。